What Is 17 In Binary
thedopedimension
Sep 22, 2025 · 6 min read
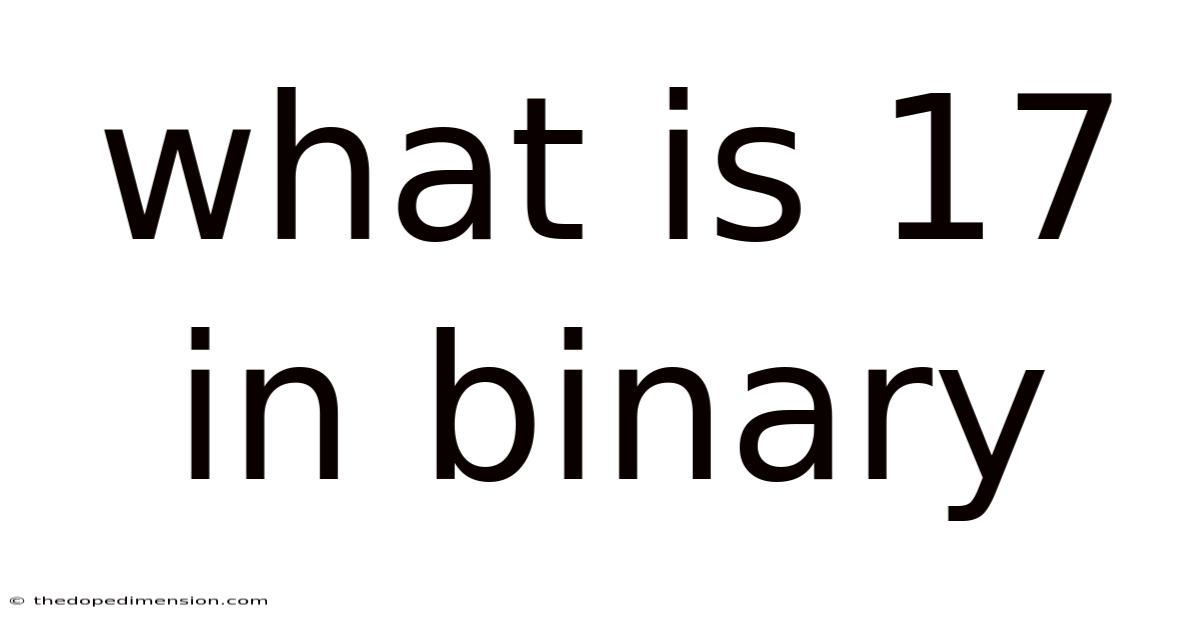
Table of Contents
What is 17 in Binary? A Deep Dive into Binary Number Systems
Understanding binary numbers is fundamental to computer science and digital electronics. This comprehensive guide will not only answer the question "What is 17 in binary?" but will also provide a thorough understanding of the binary system, its applications, and how to convert decimal numbers (like 17) to their binary equivalents. We'll explore the underlying principles, delve into the conversion process, and address frequently asked questions to solidify your grasp of this crucial concept.
Introduction to Binary Numbers
The decimal number system, the one we use daily, is based on ten digits (0-9). Each place value represents a power of 10. For example, the number 123 can be expressed as (1 x 10²) + (2 x 10¹) + (3 x 10⁰).
Binary, on the other hand, is a base-2 number system. It uses only two digits: 0 and 1. Each place value represents a power of 2. This seemingly simple system is the foundation of all digital computers and electronic devices because it's efficient and directly corresponds to the on/off states of transistors, the building blocks of modern electronics. A transistor's "on" state represents a 1, and its "off" state represents a 0.
Converting Decimal to Binary: The Process
Now, let's get to the core question: What is 17 in binary? To find the answer, we need to convert the decimal number 17 into its binary equivalent. There are two primary methods for this conversion:
Method 1: Repeated Division by 2
This is a systematic method that involves repeatedly dividing the decimal number by 2 and recording the remainders. The remainders, read in reverse order, form the binary representation.
Let's convert 17 to binary using this method:
- Divide 17 by 2: 17 ÷ 2 = 8 with a remainder of 1
- Divide 8 by 2: 8 ÷ 2 = 4 with a remainder of 0
- Divide 4 by 2: 4 ÷ 2 = 2 with a remainder of 0
- Divide 2 by 2: 2 ÷ 2 = 1 with a remainder of 0
- Divide 1 by 2: 1 ÷ 2 = 0 with a remainder of 1
Reading the remainders from bottom to top, we get 10001. Therefore, 17 in binary is 10001.
Method 2: Place Value Method
This method involves finding the largest power of 2 that is less than or equal to the decimal number and subtracting it. Then, we repeat the process with the remaining value until we reach zero.
- Find the largest power of 2 less than or equal to 17: This is 2⁴ = 16.
- Subtract 16 from 17: 17 - 16 = 1
- Find the largest power of 2 less than or equal to 1: This is 2⁰ = 1.
- Subtract 1 from 1: 1 - 1 = 0
Now, let's represent this using place values:
| 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|---|---|---|---|---|
| 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 0 | 1 |
The resulting binary number is 10001. Again, we confirm that 17 in binary is 10001.
Understanding Binary Place Values
It's crucial to understand the place values in the binary system. Unlike the decimal system where each position represents a power of 10 (1, 10, 100, 1000, etc.), the binary system uses powers of 2:
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
- 2³ = 8
- 2⁴ = 16
- 2⁵ = 32
- 2⁶ = 64
- and so on...
This means that each position to the left represents a doubling of the value. In the binary number 10001, we have:
(1 x 2⁴) + (0 x 2³) + (0 x 2²) + (0 x 2¹) + (1 x 2⁰) = 16 + 0 + 0 + 0 + 1 = 17
Applications of Binary Numbers
The binary number system is not just a mathematical curiosity; it's the backbone of modern computing. Its applications are vast and crucial:
- Computer Memory: Computers store information as sequences of 0s and 1s. Each bit (binary digit) represents a single on/off state.
- Digital Logic Circuits: Binary logic underlies the operation of digital circuits, which form the basis of computers and other electronic devices. Logic gates operate on binary inputs to produce binary outputs.
- Data Representation: Everything from text and images to audio and video is ultimately represented as binary data within a computer.
- Networking: Data transmission over networks relies on the encoding and decoding of information in binary format.
- Machine Code: The instructions executed by a computer's processor are encoded in machine code, which is a series of binary instructions.
Beyond 17: Converting Larger Decimal Numbers
The methods described above for converting 17 to binary can be applied to any decimal number, no matter how large. For example, let's convert 255:
Using the repeated division method:
- 255 ÷ 2 = 127 R 1
- 127 ÷ 2 = 63 R 1
- 63 ÷ 2 = 31 R 1
- 31 ÷ 2 = 15 R 1
- 15 ÷ 2 = 7 R 1
- 7 ÷ 2 = 3 R 1
- 3 ÷ 2 = 1 R 1
- 1 ÷ 2 = 0 R 1
Reading the remainders from bottom to top: 11111111. Therefore, 255 in decimal is 11111111 in binary.
Frequently Asked Questions (FAQ)
Q1: What is the largest number that can be represented with 8 bits?
A1: With 8 bits, you can represent 2⁸ = 256 different numbers. This ranges from 0 to 255.
Q2: Can negative numbers be represented in binary?
A2: Yes, several methods exist for representing negative numbers in binary, including two's complement, which is commonly used in computers.
Q3: How are decimal numbers with fractional parts (e.g., 17.5) converted to binary?
A3: The fractional part is converted separately by repeatedly multiplying by 2. The integer parts of the results form the binary representation of the fractional part.
Q4: What is the relationship between binary, octal, and hexadecimal?
A4: Octal (base-8) and hexadecimal (base-16) are other number systems used in computing. They are convenient shorthand representations of binary numbers because they group bits (octal groups 3 bits, hexadecimal groups 4 bits).
Q5: Why is binary so important in computing?
A5: Binary's simplicity and direct correspondence to the on/off states of transistors make it ideally suited for representing and manipulating information within digital electronic devices. This simplicity makes it computationally efficient and robust.
Conclusion
We've journeyed from a simple question – "What is 17 in binary?" – to a deeper understanding of binary number systems, their conversion methods, and their widespread applications in computing. Mastering binary is a crucial stepping stone for anyone venturing into the world of computer science, digital electronics, or any field that relies on the underlying principles of digital technology. Remember the two methods for conversion—repeated division and place value—and practice converting different decimal numbers to reinforce your understanding. The seemingly simple 0 and 1 are the powerful foundation upon which our digital world is built.
Latest Posts
Latest Posts
-
How Long Is 64 Inches
Sep 22, 2025
-
8 Min Mile To Mph
Sep 22, 2025
-
Troy Ounce To Gram Conversion
Sep 22, 2025
-
180 000 Rupees In Dollars
Sep 22, 2025
-
3 And A Half Inches
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 17 In Binary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.