55 X 35 X 25
thedopedimension
Sep 21, 2025 · 6 min read
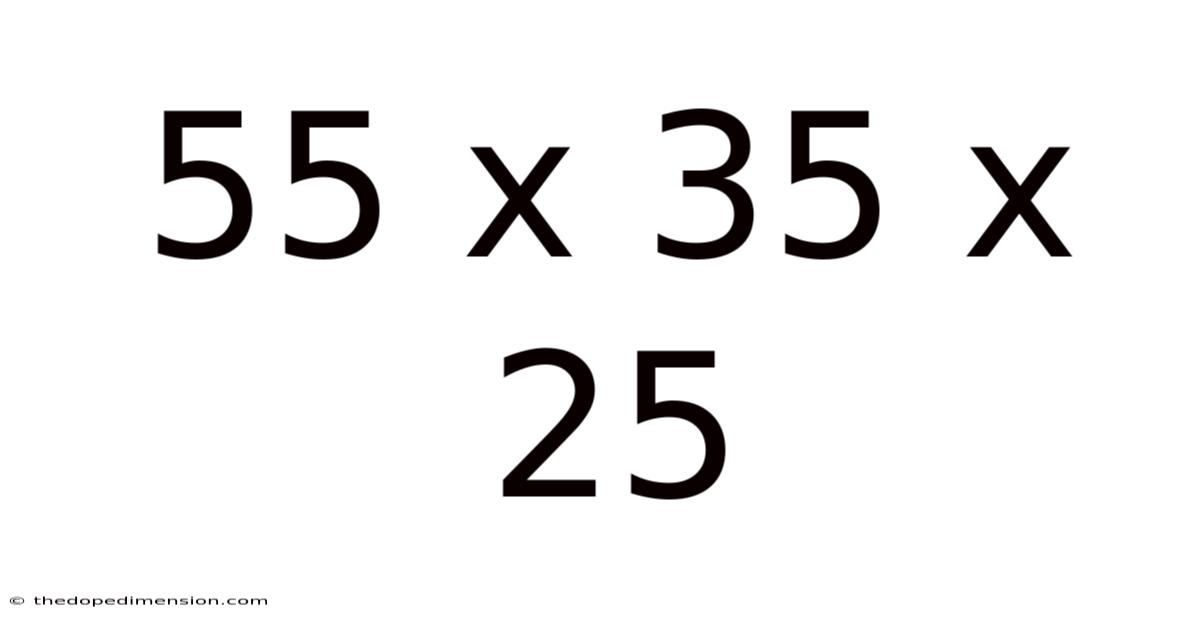
Table of Contents
Decoding 55 x 35 x 25: Exploring the Dimensions and Applications
The seemingly simple numerical sequence "55 x 35 x 25" represents a set of three-dimensional measurements, typically expressed in millimeters, centimeters, or inches, defining the length, width, and height of an object. While seemingly insignificant on its own, understanding this type of dimensional notation is crucial across numerous fields, from engineering and manufacturing to packaging and construction. This article delves into the significance of these specific dimensions (assuming they are in millimeters, a common unit in manufacturing), exploring potential applications and the underlying principles of dimensional analysis.
Understanding the Dimensions: Length, Width, and Height
The numbers 55, 35, and 25, when presented as "55 x 35 x 25," represent the length, width, and height of a rectangular prism (or cuboid). These measurements dictate the volume and surface area of the object, both crucial considerations in design and application. Let's break down what each number signifies:
-
55: This is usually considered the longest dimension, often referred to as the length. It represents the extent of the object along its primary axis.
-
35: This is often the intermediate dimension, termed the width. It indicates the extent of the object perpendicular to the length.
-
25: This is typically the shortest dimension, representing the height or depth of the object. It defines the extent of the object along the vertical axis (or the third dimension).
The order of these dimensions (length x width x height) is generally accepted but may vary depending on context. It’s crucial to understand the orientation of the object to interpret the dimensions accurately. For instance, a box with dimensions 55 x 35 x 25 could be oriented differently, yet still represent the same volume.
Calculating Volume and Surface Area
Having established the dimensions, we can calculate important properties of the object:
-
Volume: The volume of a rectangular prism is calculated by multiplying the length, width, and height. In this case, the volume is 55 mm x 35 mm x 25 mm = 48125 cubic millimeters (mm³). This can be easily converted to other units like cubic centimeters (cm³) by dividing by 1000 (1 cm³ = 1000 mm³), resulting in 48.125 cm³.
-
Surface Area: The surface area is the total area of all six faces of the rectangular prism. It is calculated as 2 * (length * width + length * height + width * height). For our example: 2 * (55 mm * 35 mm + 55 mm * 25 mm + 35 mm * 25 mm) = 2 * (1925 mm² + 1375 mm² + 875 mm²) = 8250 square millimeters (mm²). This can also be converted to square centimeters (cm²) by dividing by 100 (1 cm² = 100 mm²), resulting in 82.5 cm².
These calculations are fundamental in various applications, from determining the material required for manufacturing to calculating the shipping costs of packaged goods.
Potential Applications of 55 x 35 x 25 Dimensions
The dimensions 55 x 35 x 25 mm (or cm, depending on the scale) could represent a wide range of objects, depending on the context. Here are some potential applications:
-
Electronics Packaging: This size could be suitable for packaging smaller electronic components, such as circuit boards, power supplies, or small gadgets. The dimensions could accommodate internal compartments for organized packing.
-
Industrial Components: In manufacturing, components of this size might be found in various machines or systems. They could be housing units, enclosures, or parts with specific internal structures.
-
Custom-Made Boxes or Containers: Many businesses require custom-sized boxes for specific products. These dimensions could be perfectly tailored for a specific item's safe and efficient packaging.
-
Medical Device Components: The precision required in medical devices might necessitate components with these precise dimensions for optimal functionality and integration.
-
3D-Printed Objects: The dimensions are within the feasible range for many 3D printers, making it possible to create objects with this specific shape and size.
-
Prototype Modeling: Designers and engineers often create prototypes with specified dimensions. 55 x 35 x 25 mm could represent the dimensions of a prototype component or product casing.
The specific application depends heavily on the material and intended use of the object. For example, a 55 x 35 x 25 mm object made of metal would likely have a different application than one made of plastic or wood.
The Importance of Dimensional Accuracy
In engineering and manufacturing, precision is paramount. Even slight deviations from the specified dimensions (55 x 35 x 25 mm) can impact the functionality and performance of a product. Therefore, accurate measurement and manufacturing techniques are crucial to ensure the final product meets the required specifications. Tolerance is a key concept in manufacturing, defining the acceptable range of variation from the nominal dimensions.
Dimensional Analysis: Beyond the Numbers
Understanding the 55 x 35 x 25 dimensions requires going beyond simple numerical values. Dimensional analysis involves examining the units and the relationship between dimensions to understand the physical significance of the measurements. For example, understanding the volume (in cubic millimeters or centimeters) allows us to estimate material requirements, weight, and other crucial aspects of the object's properties. Similarly, the surface area helps determine factors like heat dissipation, paint coverage, and packaging design.
Scale and Unit Conversions
It’s critical to pay attention to the units of measurement. 55 x 35 x 25 could refer to millimeters, centimeters, inches, or even other units. Accurate unit conversion is essential to avoid errors in calculations and interpretations. Always specify the units clearly to avoid ambiguity. Common conversion factors include:
- 1 cm = 10 mm
- 1 inch = 25.4 mm
Correctly converting units is essential for seamless communication and accurate calculations in engineering, design, and manufacturing.
Frequently Asked Questions (FAQ)
Q: What is the volume of an object with dimensions 55 x 35 x 25 mm?
A: The volume is 55 mm * 35 mm * 25 mm = 48125 cubic millimeters (mm³), or 48.125 cubic centimeters (cm³).
Q: What is the surface area of an object with dimensions 55 x 35 x 25 mm?
A: The surface area is 2 * (55 mm * 35 mm + 55 mm * 25 mm + 35 mm * 25 mm) = 8250 square millimeters (mm²), or 82.5 square centimeters (cm²).
Q: What materials could be used to create an object with these dimensions?
A: Many materials are possible, including various plastics, metals (aluminum, steel), wood, and composites. The choice depends on the application and desired properties (strength, weight, cost, etc.).
Q: Are these dimensions standard for any specific product or industry?
A: These dimensions aren't standard for any particular product. However, they fall within a range that's suitable for numerous applications, as discussed earlier.
Q: How important is precision in manufacturing objects with these dimensions?
A: Precision is vital, especially in applications requiring tight tolerances. Even small deviations can affect functionality and performance.
Conclusion
The seemingly simple sequence "55 x 35 x 25" reveals a wealth of information when viewed through the lens of dimensional analysis. Understanding these dimensions, calculating the volume and surface area, and recognizing potential applications highlight the crucial role of precise measurements in various industries. Whether in electronics packaging, industrial manufacturing, or 3D printing, accurate dimensional specifications are essential for successful design and production. The ability to interpret and work with these measurements effectively is a fundamental skill across numerous engineering and design disciplines. Remember to always consider the units of measurement and the implications of tolerances for ensuring accuracy and successful project completion.
Latest Posts
Latest Posts
-
40 Pounds In Aud Dollars
Sep 21, 2025
-
40 Quarts How Many Gallons
Sep 21, 2025
-
500 000 Dkk To Usd
Sep 21, 2025
-
Currency Dirhams To Peso Today
Sep 21, 2025
-
10000 Iranian Rial To Usd
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 55 X 35 X 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.