3.14 X 3 X 3
thedopedimension
Sep 25, 2025 · 6 min read
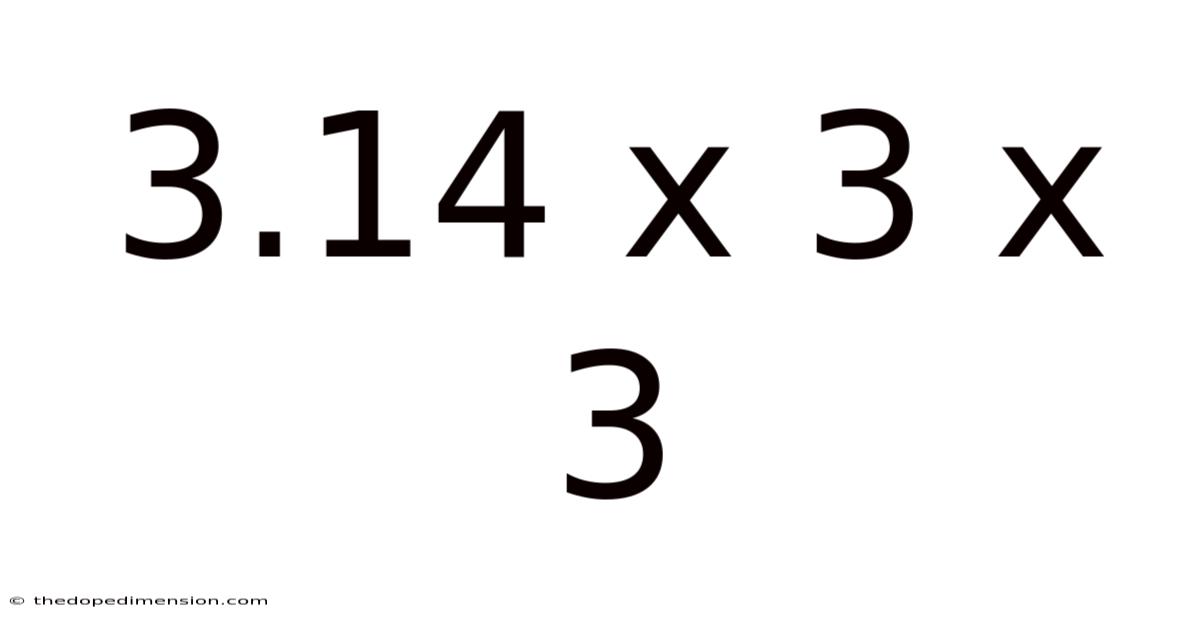
Table of Contents
Unraveling the Mystery: A Deep Dive into 3.14 x 3 x 3
The seemingly simple calculation, 3.14 x 3 x 3, might appear unremarkable at first glance. However, this expression opens a door to a fascinating exploration of mathematics, geometry, and the fundamental constant π (pi). This article will delve into the meaning behind this calculation, its relationship to circles and cylinders, practical applications, and even touch upon some related mathematical concepts. We will unpack the significance of each number and the result they produce together, providing a comprehensive understanding suitable for learners of all levels.
Understanding the Components: Pi, Radius, and Area
The expression 3.14 x 3 x 3 can be broken down into its constituent parts to understand its deeper meaning. Let's analyze each component:
-
3.14 (π or Pi): This is the approximate value of pi, a mathematical constant representing the ratio of a circle's circumference to its diameter. Pi is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on infinitely without repeating. The value 3.14 is a commonly used approximation, sufficient for many practical calculations.
-
3: This number represents a radius. In geometry, the radius of a circle is the distance from the center of the circle to any point on its circumference. In our calculation, we're dealing with a circle (or a cylinder, as we'll see later) with a radius of 3 units. The units could be anything – centimeters, meters, inches, etc. – but the numerical relationship remains the same.
-
3: This number, again, represents the same radius. The repetition highlights the calculation's specific application in finding the area related to circles.
The Calculation: Unveiling the Area of a Circle
When we multiply π (approximately 3.14) by the radius squared (3 x 3 = 9), we are essentially calculating the area of a circle. The formula for the area of a circle is:
Area = πr²
Where:
- A represents the area
- π represents pi (approximately 3.14)
- r represents the radius of the circle
Therefore, 3.14 x 3 x 3 = 28.26 is the approximate area of a circle with a radius of 3 units. This area is measured in square units (e.g., square centimeters, square meters).
Expanding the Horizons: Cylinders and Volume
The calculation takes on a new dimension when we consider three-dimensional shapes. Imagine a cylinder with a circular base. The same calculation, 3.14 x 3 x 3, forms a crucial part of calculating the volume of a cylinder.
The formula for the volume of a cylinder is:
Volume = πr²h
Where:
- V represents the volume
- π represents pi (approximately 3.14)
- r represents the radius of the circular base
- h represents the height of the cylinder
In our case, we've already calculated πr² (3.14 x 3 x 3 = 28.26), which represents the area of the circular base. If the height of the cylinder is 1 unit, then the volume would be approximately 28.26 cubic units. If the height were 2 units, the volume would double to approximately 56.52 cubic units, and so on. The calculation 3.14 x 3 x 3 therefore lays the foundation for calculating the volume of any cylinder with a radius of 3 units.
Practical Applications: From Engineering to Baking
The seemingly simple calculation, 3.14 x 3 x 3, finds numerous applications in various fields:
-
Engineering and Architecture: Calculating the area and volume of circular structures is fundamental in engineering and architecture. From designing water tanks and pipes to calculating the material needed for building domes and columns, this calculation provides essential data for construction projects.
-
Manufacturing: Manufacturing processes often involve circular components. Determining the surface area or volume of these components is critical for material estimation, production planning, and quality control.
-
Science: Many scientific experiments and calculations involve circular or cylindrical shapes. This calculation plays a role in fields like fluid dynamics, physics, and chemistry.
-
Everyday Life: Even in everyday life, we may encounter situations where this calculation is relevant. For example, determining the amount of paint needed to cover a circular wall or calculating the volume of a cylindrical container are practical applications.
Beyond the Basics: Delving into More Advanced Concepts
The calculation 3.14 x 3 x 3 provides a springboard to explore more advanced mathematical concepts:
-
Integration and Calculus: The calculation of the area of a circle is a basic application of integral calculus. More complex shapes require more sophisticated integration techniques, but the fundamental concept remains the same: breaking down complex shapes into smaller, simpler shapes whose areas can be easily calculated.
-
Solid Geometry and Three-Dimensional Shapes: The extension of the calculation to cylinder volumes provides an introduction to solid geometry. Understanding volumes and surface areas of various three-dimensional shapes is crucial in many scientific and engineering disciplines.
-
Numerical Analysis and Approximation: The use of 3.14 as an approximation of π highlights the importance of numerical analysis. Different levels of precision are required depending on the application, and understanding error estimations is crucial for accurate results.
Frequently Asked Questions (FAQ)
Q: Why is 3.14 used instead of the full value of pi?
A: Pi is an irrational number, meaning its decimal representation goes on infinitely. Using 3.14 is a convenient approximation that provides sufficient accuracy for many practical applications. For more precise calculations, more digits of pi can be used.
Q: What are the units involved in the calculation?
A: The units depend on the context. If the radius is 3 centimeters, then the area is calculated in square centimeters, and the volume of a cylinder (if applicable) is in cubic centimeters. The units are always squared for area and cubed for volume.
Q: Can this calculation be used for other shapes?
A: This specific calculation, 3.14 x 3 x 3, directly applies to circles and cylinders. However, the principles behind it – using π and the radius – are fundamental to calculating the areas and volumes of many other shapes.
Q: What if the radius was a different number?
A: Simply replace the '3' in the calculation with the new radius value. The area will be π multiplied by the square of the new radius.
Conclusion: The Power of a Simple Calculation
The calculation 3.14 x 3 x 3, while seemingly simple, encapsulates a wealth of mathematical concepts and practical applications. From understanding the fundamental constant π to calculating the area of a circle and the volume of a cylinder, this expression offers a gateway to exploring geometry, calculus, and various scientific and engineering fields. Its widespread applicability underscores the power and elegance of mathematics in describing and understanding our world. By understanding the underlying principles, we can appreciate the profound implications of this seemingly simple numerical operation and apply it to solve a multitude of problems across diverse disciplines. The journey from a straightforward calculation to a deeper comprehension of mathematical principles highlights the beauty and utility of mathematical exploration.
Latest Posts
Latest Posts
-
1 4 Of An Hour Is
Sep 25, 2025
-
139 Sq Meters To Feet
Sep 25, 2025
-
0 5 Ppm To Mg Kg
Sep 25, 2025
-
Convert 420 Ml To Ounces
Sep 25, 2025
-
10 500 Yen To Usd
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3.14 X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.