27 7 As A Decimal
thedopedimension
Sep 23, 2025 · 6 min read
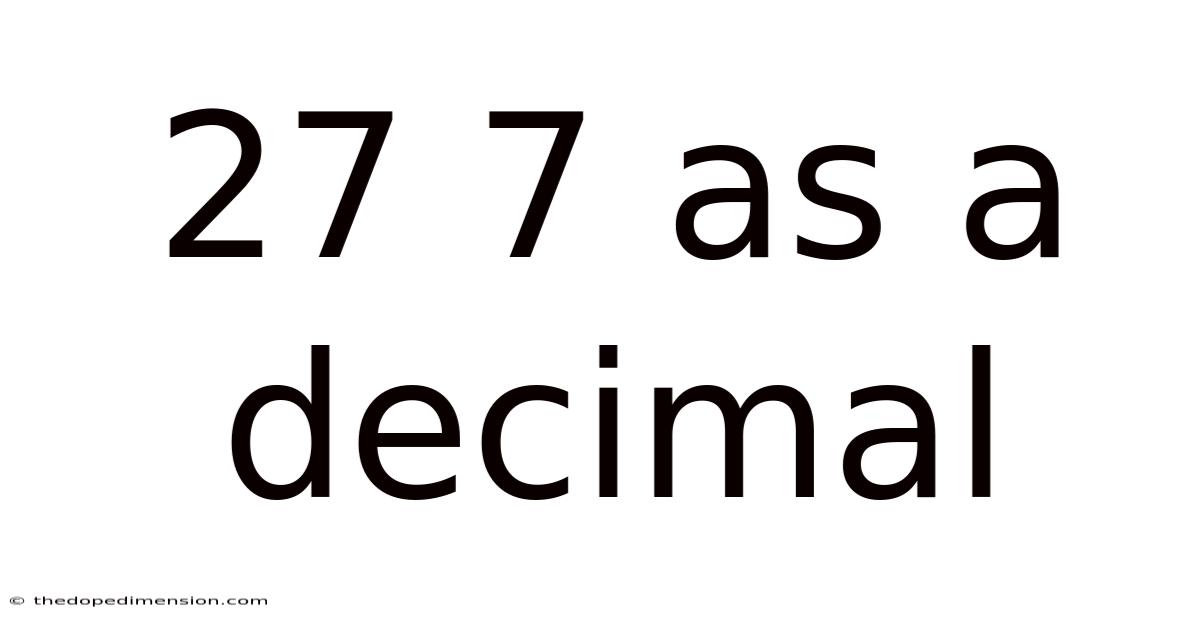
Table of Contents
Unveiling the Mystery: 27/7 as a Decimal
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This article will delve into the process of converting the fraction 27/7 into its decimal equivalent, exploring the various methods involved, explaining the underlying mathematical principles, and addressing common questions and misconceptions. We'll go beyond a simple answer, providing a comprehensive understanding that will empower you to tackle similar conversions with confidence.
Understanding Fractions and Decimals
Before diving into the conversion of 27/7, let's establish a firm grasp of the concepts involved. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a number based on powers of 10. It uses a decimal point to separate the whole number part from the fractional part. Converting a fraction to a decimal essentially means expressing the fractional part of the whole using the decimal system.
Method 1: Long Division
The most straightforward method to convert 27/7 to a decimal is through long division. This method involves dividing the numerator (27) by the denominator (7).
-
Set up the long division: Write 27 as the dividend and 7 as the divisor.
-
Divide: 7 goes into 27 three times (7 x 3 = 21). Write 3 above the 7 in the dividend.
-
Subtract: Subtract 21 from 27, leaving a remainder of 6.
-
Bring down a zero: Add a decimal point to the quotient (the number you're writing above) and a zero to the remainder. Now you have 60.
-
Continue dividing: 7 goes into 60 eight times (7 x 8 = 56). Write 8 after the decimal point in the quotient.
-
Subtract again: Subtract 56 from 60, leaving a remainder of 4.
-
Repeat the process: Add another zero to the remainder, making it 40. 7 goes into 40 five times (7 x 5 = 35). Write 5 in the quotient.
-
Subtract and repeat: Subtract 35 from 40, leaving a remainder of 5. Adding another zero gives 50. 7 goes into 50 seven times (7 x 7 = 49). Write 7 in the quotient.
-
Observe the pattern: You'll notice a repeating pattern in the remainder: 6, 4, 5, 1, 3, 2, 6… This indicates that the decimal representation of 27/7 is a repeating decimal.
Therefore, 27/7 ≈ 3.857142857142… The digits 857142 repeat infinitely.
Method 2: Using a Calculator
A much quicker method, especially for more complex fractions, is to use a calculator. Simply enter 27 ÷ 7 and press the equals button. Most calculators will display the decimal equivalent, showing either a rounded version or, if capable, the repeating decimal with a notation to indicate its repetitive nature (e.g., 3.857142857142...).
Understanding Repeating Decimals
The result of 27/7 highlights an important concept: repeating decimals. These are decimals where one or more digits repeat infinitely. In mathematical notation, we often represent repeating decimals using a bar over the repeating digits. For example, the decimal representation of 27/7 can be written as 3.857142̅. The bar indicates that the sequence 857142 repeats endlessly. Not all fractions result in repeating decimals; some terminate (end after a finite number of digits). Whether a fraction results in a terminating or repeating decimal depends on the prime factorization of the denominator. If the denominator's prime factorization contains only 2s and/or 5s, the decimal will terminate. Otherwise, it will repeat.
The Significance of the Remainder
In the long division method, the remainder plays a crucial role. If the remainder eventually becomes zero, the decimal terminates. However, if the remainder repeats, as in the case of 27/7, the decimal will repeat infinitely. The repeating sequence of remainders directly corresponds to the repeating sequence of digits in the decimal representation. This is a fundamental concept in understanding the relationship between fractions and their decimal equivalents.
Practical Applications of Decimal Conversions
Converting fractions to decimals is vital in numerous practical applications across various fields:
- Engineering and Physics: Accurate calculations in engineering and physics often require converting fractions to decimals for precise measurements and computations.
- Finance and Accounting: Calculating interest rates, percentages, and profits often involves working with decimal numbers derived from fractions.
- Computer Science: Representing fractional values in computer programs requires converting them to decimal equivalents.
- Everyday Life: Many everyday calculations, such as measuring ingredients in cooking or calculating distances, may involve converting fractions to decimals for easier comprehension and calculation.
Common Mistakes and Misconceptions
Several common mistakes can occur when converting fractions to decimals:
- Incorrect placement of the decimal point: Careless placement of the decimal point can lead to significant errors in the calculation.
- Truncation instead of rounding: Stopping the division process before the repeating pattern is fully established leads to an inaccurate representation of the decimal.
- Misunderstanding repeating decimals: Failing to recognize and correctly represent repeating decimals can result in inaccurate calculations.
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to decimals?
A1: Yes, all fractions can be converted to decimals. However, some will result in terminating decimals, while others will result in repeating decimals.
Q2: How can I round a repeating decimal?
A2: Rounding a repeating decimal depends on the desired level of accuracy. You decide how many decimal places you need, and then round the last digit according to standard rounding rules (if the next digit is 5 or greater, round up; otherwise, round down).
Q3: What is the difference between a terminating and a repeating decimal?
A3: A terminating decimal ends after a finite number of digits. A repeating decimal continues infinitely with a repeating sequence of digits.
Q4: Is there a way to predict if a fraction will result in a terminating or repeating decimal?
A4: Yes. If the denominator of the fraction, when simplified, contains only prime factors of 2 and/or 5, the decimal will terminate. Otherwise, it will repeat.
Conclusion
Converting 27/7 to a decimal, approximately 3.857142̅, provides a valuable opportunity to deepen our understanding of fractions, decimals, and the fundamental mathematical operations connecting them. While a calculator offers a quick solution, mastering long division provides a deeper appreciation of the underlying principles. Understanding repeating decimals and their representation is essential for accurate calculations in various fields. By mastering these concepts, you equip yourself with a crucial skill applicable across numerous mathematical and real-world scenarios. Remember to pay close attention to detail during long division, particularly the placement of the decimal point and the identification of repeating patterns. With practice and a clear understanding of the methods involved, you can confidently tackle any fraction-to-decimal conversion.
Latest Posts
Latest Posts
-
112 Km H To Mph
Sep 23, 2025
-
180 Ft Lb Torque Wrench
Sep 23, 2025
-
160 Cm Height In Feet
Sep 23, 2025
-
5 9 Is How Many Inches
Sep 23, 2025
-
Whats Bigger Bits Or Bytes
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 27 7 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.