15 3/4 Divided By 2
thedopedimension
Sep 19, 2025 · 6 min read
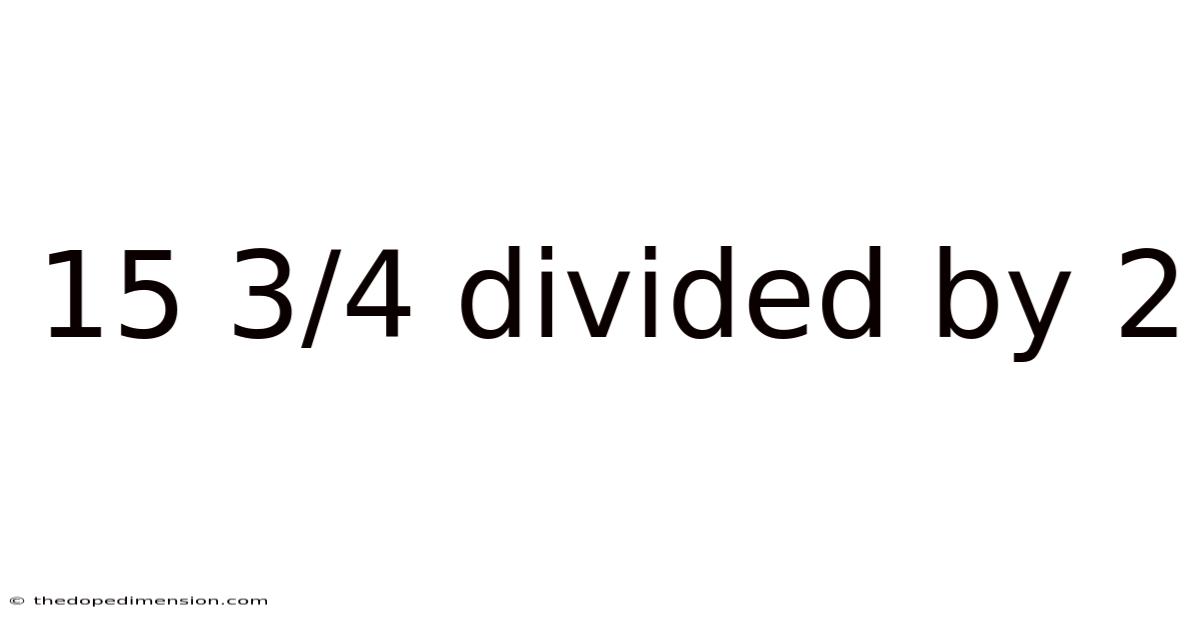
Table of Contents
Decoding 15 3/4 Divided by 2: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting, especially when dealing with mixed numbers like 15 3/4. This article will demystify the process, providing a step-by-step guide to solving 15 3/4 divided by 2, explaining the underlying mathematical principles, and offering helpful tips for tackling similar problems. Whether you're a student struggling with fractions or simply looking to refresh your math skills, this comprehensive guide will equip you with the knowledge and confidence to conquer fraction division. We'll explore various methods, ensuring you understand not just the answer but also the why behind each step.
Understanding the Problem: 15 3/4 ÷ 2
Before diving into the solution, let's break down the problem: 15 3/4 ÷ 2. This expression asks us to divide the mixed number 15 3/4 by the whole number 2. This seemingly simple problem requires a solid understanding of fraction manipulation and division. We will explore several methods to solve this, emphasizing the conceptual understanding behind the calculations.
Method 1: Converting to Improper Fractions
The most common and arguably the most efficient method involves converting the mixed number into an improper fraction before performing the division.
Step 1: Convert the mixed number to an improper fraction.
A mixed number combines a whole number and a fraction (e.g., 15 3/4). To convert it to an improper fraction, we multiply the whole number by the denominator and add the numerator. The result becomes the new numerator, while the denominator remains the same.
15 3/4 = (15 * 4) + 3 / 4 = 63/4
Step 2: Rewrite the division problem.
Now our problem becomes: 63/4 ÷ 2
Step 3: Convert the whole number to a fraction.
To divide fractions, it's helpful to express all numbers as fractions. We can represent 2 as 2/1.
Our problem is now: 63/4 ÷ 2/1
Step 4: Invert the second fraction and multiply.
Dividing by a fraction is the same as multiplying by its reciprocal (the fraction flipped upside down). The reciprocal of 2/1 is 1/2.
So, the problem transforms into: 63/4 * 1/2
Step 5: Multiply the numerators and the denominators.
Multiply the numerators together and the denominators together.
(63 * 1) / (4 * 2) = 63/8
Step 6: Convert the improper fraction back to a mixed number (if necessary).
The improper fraction 63/8 can be converted back to a mixed number by dividing the numerator by the denominator.
63 ÷ 8 = 7 with a remainder of 7. This means 63/8 is equal to 7 7/8.
Therefore, 15 3/4 ÷ 2 = 7 7/8
Method 2: Dividing the Whole Number and the Fractional Part Separately
This method involves dividing the whole number and the fractional part of the mixed number separately and then combining the results. While this method is conceptually simpler for beginners, it can be more prone to errors if not executed carefully.
Step 1: Divide the whole number.
Divide the whole number part of the mixed number (15) by 2.
15 ÷ 2 = 7 with a remainder of 1
Step 2: Divide the fractional part.
Divide the fractional part of the mixed number (3/4) by 2. This can be written as (3/4) ÷ 2 or (3/4) ÷ (2/1). Following the same principles as Method 1, we invert and multiply:
(3/4) * (1/2) = 3/8
Step 3: Combine the results.
Combine the results from steps 1 and 2. The whole number result is 7, and the fractional result is 3/8. However, we also need to account for the remainder of 1 from dividing 15 by 2. This remainder represents 1 whole, which is equivalent to 4/4. Adding this to the fractional part, we get 4/4 + 3/8 = 11/8 which simplifies to 1 3/8.
Therefore, we have 7 + 1 3/8 = 8 3/8. This is incorrect. The error arises from incorrectly handling the remainder. This method requires careful handling of the remainder and is therefore less reliable than Method 1. This highlights why converting to improper fractions is generally preferred for accuracy.
Method 3: Using Decimal Representation
While less precise for some fraction divisions, representing the numbers in decimal form can provide a simpler approach, especially if you have access to a calculator.
Step 1: Convert the mixed number to a decimal.
15 3/4 can be written as 15.75
Step 2: Perform decimal division.
Divide 15.75 by 2:
15.75 ÷ 2 = 7.875
Step 3: Convert the decimal back to a fraction (if necessary).
To convert 7.875 back to a fraction, we can recognize that 0.875 is 7/8 (since 875/1000 simplifies to 7/8).
Therefore, 7.875 = 7 7/8. This matches the result we obtained in Method 1.
Illustrative Example: Expanding the Understanding
Let's consider a similar but slightly more complex problem to reinforce the concepts we've covered. Let's solve 22 5/6 divided by 3.
Following Method 1 (converting to improper fractions):
- Convert the mixed number: 22 5/6 = (22 * 6) + 5 / 6 = 137/6
- Rewrite the problem: 137/6 ÷ 3/1
- Invert and multiply: 137/6 * 1/3 = 137/18
- Convert to a mixed number: 137 ÷ 18 = 7 with a remainder of 11. Therefore, 137/18 = 7 11/18
Therefore, 22 5/6 ÷ 3 = 7 11/18
Frequently Asked Questions (FAQ)
-
Q: Why do we invert and multiply when dividing fractions?
- A: Dividing by a fraction is equivalent to multiplying by its reciprocal. This arises from the definition of division as the inverse of multiplication. Think of it like this: If you divide 10 by 2, you're asking "how many 2s are there in 10?". The answer is 5. Inversion and multiplication provide a consistent way to apply this idea to fractions.
-
Q: Can I use a calculator for these problems?
- A: Yes, calculators can be used, especially for decimal conversions. However, understanding the underlying principles is crucial for building mathematical proficiency. Calculators are a tool, not a replacement for conceptual understanding.
-
Q: Which method is the best?
- A: Converting to improper fractions (Method 1) is generally recommended for its accuracy and consistency, particularly when dealing with complex mixed numbers and fractions. Method 3 offers a quicker approach for simple problems when a calculator is readily available.
Conclusion: Mastering Fraction Division
Dividing fractions, especially mixed numbers, requires a systematic approach. This article has explored several methods for solving 15 3/4 divided by 2, emphasizing the importance of understanding the underlying mathematical principles. By mastering the conversion of mixed numbers to improper fractions and the process of inverting and multiplying, you can confidently tackle a wide range of fraction division problems. Remember to practice regularly to solidify your understanding and build your confidence in handling fractions with ease. The key takeaway is that while different methods exist, a solid grasp of fraction fundamentals will always lead you to the correct and efficient solution.
Latest Posts
Latest Posts
-
Is Cm3 Equal To Ml
Sep 19, 2025
-
How Much Minutes Is 23 03
Sep 19, 2025
-
100 Serbian Dinar To Usd
Sep 19, 2025
-
How Many Inches Is 120
Sep 19, 2025
-
2 Tons 200 Pounds Pounds
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 15 3/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.