1/3 C + 1/3 C
thedopedimension
Sep 20, 2025 · 6 min read
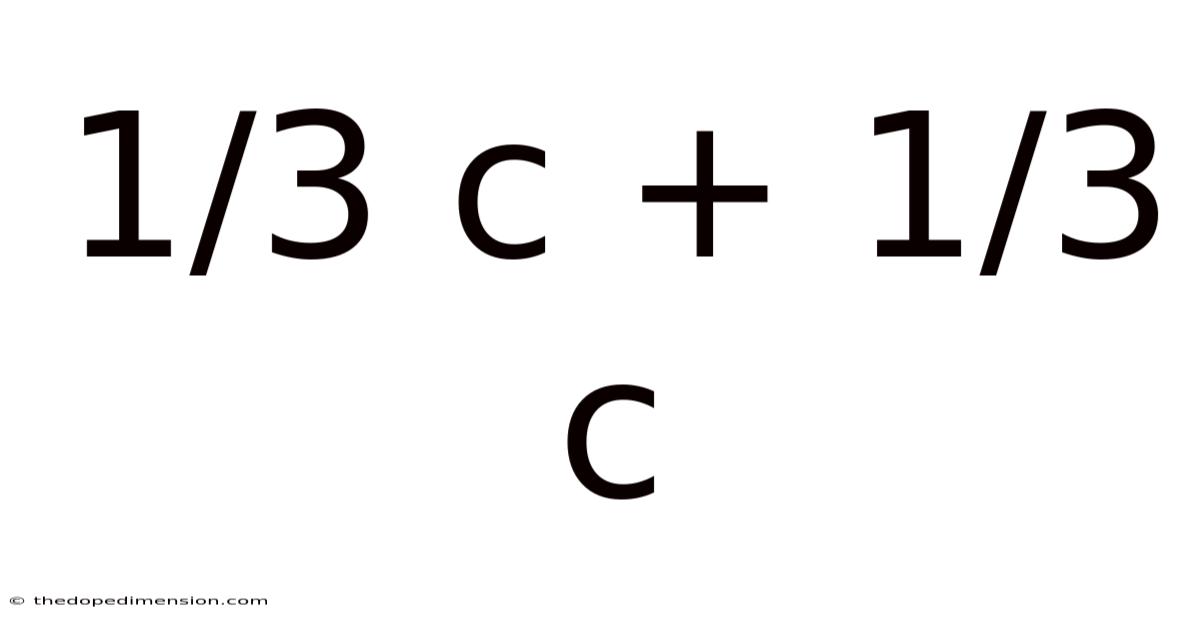
Table of Contents
Decoding the Simple Sum: 1/3 c + 1/3 c = ? A Deep Dive into Fractions and Culinary Math
Adding fractions might seem like a simple task, especially when dealing with seemingly straightforward numbers like 1/3. However, understanding the underlying principles of fraction addition is crucial, not only for acing math tests but also for everyday applications like cooking and baking. This article will explore the seemingly simple equation of 1/3 c + 1/3 c, delving into the mathematical processes, providing practical examples, and addressing common misconceptions. This exploration will go beyond the basic answer, empowering you with a deeper understanding of fractions and their relevance in various contexts.
Understanding Fractions: A Quick Refresher
Before we tackle our specific problem, let's revisit the fundamentals of fractions. A fraction represents a part of a whole. It consists of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
In our equation, 1/3 c, '1' is the numerator and '3' is the denominator. This means we have one part out of a total of three equal parts (of a cup, in this culinary context).
Adding Fractions with Common Denominators: The Simple Case
Adding fractions is straightforward when the denominators are the same. In such cases, we simply add the numerators and keep the denominator unchanged. This is precisely the scenario we encounter with 1/3 c + 1/3 c:
1/3 c + 1/3 c = (1 + 1)/3 c = 2/3 c
Therefore, the answer to 1/3 c + 1/3 c is 2/3 c. This means if you add one-third of a cup to another one-third of a cup, you obtain two-thirds of a cup.
Expanding the Concept: Adding Fractions in Baking and Cooking
The seemingly simple addition of 1/3 c + 1/3 c holds significant practical value in culinary applications. Many recipes rely on precise measurements, and understanding fraction addition is crucial for achieving the desired results. Imagine you're following a recipe that calls for 1/3 cup of sugar for one part of the recipe and another 1/3 cup for a second part. Knowing that 1/3 c + 1/3 c = 2/3 c allows you to easily measure the total amount of sugar needed without resorting to multiple smaller measurements.
Beyond the Basics: Adding Fractions with Different Denominators
While our initial problem involved fractions with the same denominator, let's expand our understanding to include scenarios where the denominators differ. For example, consider adding 1/3 c and 1/4 c. In such cases, we need to find a common denominator – a number that is divisible by both denominators.
For 1/3 and 1/4, the least common denominator (LCD) is 12. We then convert each fraction to have a denominator of 12:
1/3 = (1 x 4)/(3 x 4) = 4/12 1/4 = (1 x 3)/(4 x 3) = 3/12
Now, we can add the fractions:
4/12 + 3/12 = (4 + 3)/12 = 7/12
Therefore, 1/3 c + 1/4 c = 7/12 c. This example highlights the importance of finding a common denominator before adding fractions with different denominators. This skill is invaluable for more complex baking or cooking recipes that might require precise measurements with a variety of fractional ingredients.
Practical Applications: Real-World Scenarios Involving Fractions
The principles of fraction addition aren't confined to the kitchen. They permeate various aspects of daily life:
-
Construction and Engineering: Calculating material quantities, determining precise dimensions, and ensuring accurate measurements are crucial for construction projects. Understanding fractions is paramount for ensuring structural integrity and achieving the desired outcomes.
-
Sewing and Tailoring: Precise measurements are essential in sewing and tailoring. Calculating fabric quantities, adjusting patterns, and ensuring proper fit all rely on a strong understanding of fractions.
-
Finance and Budgeting: Managing finances effectively often involves dealing with fractions, especially when working with percentages, discounts, and interest rates. Understanding fractions improves financial literacy and aids in making informed financial decisions.
-
Data Analysis and Statistics: Fractions are frequently used in data analysis and statistics. Representing proportions, calculating probabilities, and interpreting statistical data all require a good grasp of fractional concepts.
Addressing Common Misconceptions about Fraction Addition
Several common misconceptions can hinder one's understanding of fraction addition:
-
Adding denominators: A common mistake is to add both the numerators and the denominators. Remember, we only add the numerators when the denominators are the same; the denominator remains unchanged.
-
Ignoring the common denominator: When adding fractions with different denominators, forgetting to find a common denominator before adding the numerators leads to incorrect results.
-
Simplifying fractions: After adding fractions, always simplify the resulting fraction to its lowest terms. For example, 6/12 can be simplified to 1/2 by dividing both the numerator and the denominator by their greatest common divisor (6).
Frequently Asked Questions (FAQ)
Q1: What if I need to add more than two fractions?
A1: The same principles apply. If the fractions have a common denominator, simply add the numerators. If they have different denominators, find the least common denominator (LCD) first, convert each fraction to have the LCD, and then add the numerators.
Q2: How do I simplify a fraction?
A2: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator. Divide both the numerator and the denominator by the GCD. The resulting fraction is the simplified form.
Q3: What if the resulting fraction is an improper fraction (numerator is larger than the denominator)?
A3: An improper fraction can be converted into a mixed number (a whole number and a fraction). Divide the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the fractional part, with the denominator remaining the same.
Q4: Are there any online tools or calculators to help with fraction addition?
A4: Yes, many online calculators and tools are available to assist with fraction addition and other mathematical operations. These tools can be helpful for checking your work and gaining further understanding.
Conclusion: Mastering Fractions for a More Complete Understanding
This in-depth exploration of 1/3 c + 1/3 c has moved beyond a simple arithmetic problem. It has highlighted the broader importance of understanding fractions and their applications in various aspects of life, particularly in fields requiring precision and accuracy. Mastering fraction addition is not merely about solving mathematical problems; it's about developing a crucial skillset that enhances problem-solving capabilities and promotes a deeper appreciation for mathematical concepts. By understanding the underlying principles, we can confidently tackle more complex fractional calculations and apply this knowledge in various practical contexts, from baking a perfect cake to calculating the dimensions of a building. The seemingly simple addition of 1/3 c + 1/3 c serves as a gateway to a richer understanding of fractions and their profound impact on our daily lives.
Latest Posts
Latest Posts
-
10 Malaysian Ringgit To Usd
Sep 20, 2025
-
How Much Is 15 Gram
Sep 20, 2025
-
Inch Symbol Vs Foot Symbol
Sep 20, 2025
-
1 Pound To Philippine Peso
Sep 20, 2025
-
1 Pound Sterling To Naira
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/3 C + 1/3 C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.