0.1 Percent As A Decimal
thedopedimension
Sep 18, 2025 · 5 min read
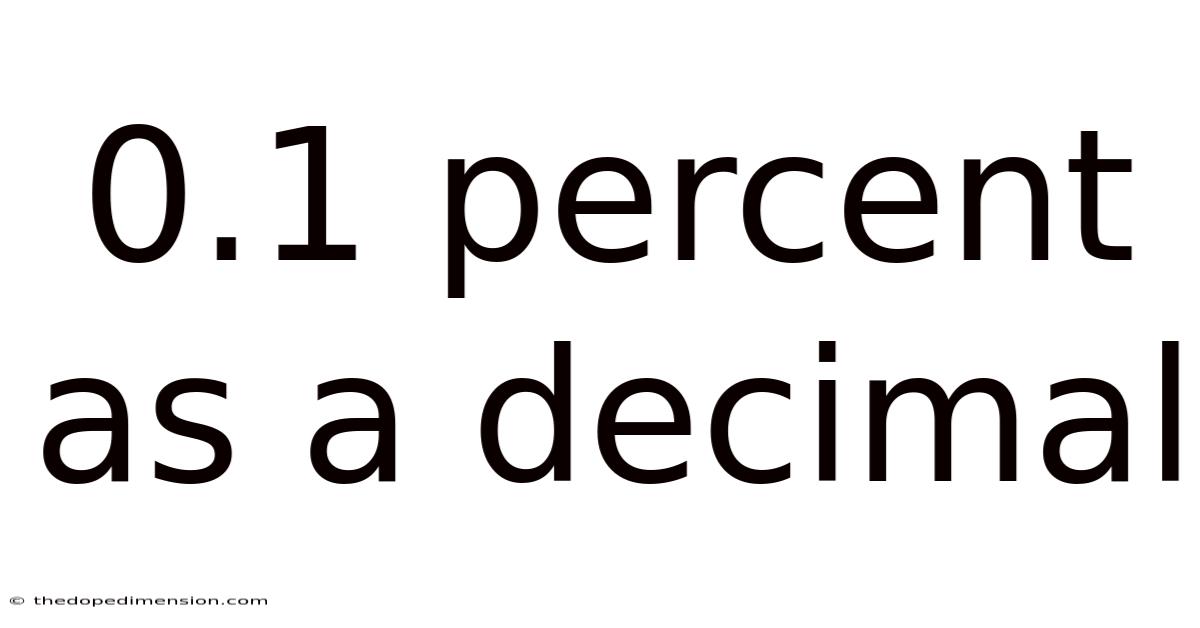
Table of Contents
Understanding 0.1 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and crucial for numerous applications in everyday life, from calculating discounts to understanding financial reports. This article will delve into the specifics of converting 0.1 percent into its decimal form, explaining the process clearly and comprehensively. We'll cover the underlying principles, explore practical examples, and address common questions, ensuring you gain a solid grasp of this concept. By the end, you'll be confident in converting percentages to decimals and vice-versa.
What is a Percentage?
A percentage (%) represents a fraction of 100. It signifies a portion or proportion out of a whole, where the whole is considered 100%. For example, 50% means 50 out of 100, or one-half (½). Percentages are widely used to express proportions, ratios, and rates in various contexts, including finance, statistics, and everyday calculations.
Converting Percentages to Decimals: The Fundamental Principle
The key to converting a percentage to a decimal is understanding that the percentage sign (%) essentially means "divided by 100". Therefore, to convert any percentage to its decimal equivalent, you simply divide the percentage value by 100. Alternatively, and often more efficiently, you can move the decimal point two places to the left.
Let's illustrate with a simple example: 25%
- Method 1: Division: 25% = 25 ÷ 100 = 0.25
- Method 2: Decimal Point Shift: 25. (Move the decimal point two places to the left) = 0.25
Both methods yield the same result: 25% is equivalent to the decimal 0.25.
Converting 0.1 Percent to a Decimal
Now, let's apply this principle to the specific case of 0.1%. Following the same methods:
- Method 1: Division: 0.1% = 0.1 ÷ 100 = 0.001
- Method 2: Decimal Point Shift: 0.1 (Move the decimal point two places to the left) = 0.001
Therefore, 0.1% as a decimal is 0.001.
Why is Understanding this Conversion Important?
The ability to convert percentages to decimals is essential for various reasons:
- Mathematical Calculations: Many mathematical operations, such as multiplication and division, are easier to perform with decimals than with percentages. Converting percentages to decimals allows for simpler and more accurate calculations.
- Financial Applications: In finance, understanding decimal equivalents of percentages is crucial for calculating interest rates, discounts, taxes, and investment returns.
- Data Analysis: Statistical analysis often requires working with decimal values. Converting percentages into decimals simplifies data manipulation and interpretation.
- Spreadsheets and Software: Most spreadsheet software and other applications handle decimal values more readily than percentages. This conversion is necessary for seamless data entry and calculation.
- Scientific and Engineering Applications: In scientific and engineering fields, precise calculations often involve decimal values, making the ability to convert percentages essential.
Practical Examples: Applying the Conversion
Let's look at some practical examples showcasing the use of 0.001 (the decimal equivalent of 0.1%):
Example 1: Calculating a Discount
A store offers a 0.1% discount on all items. If an item costs $100, the discount amount is calculated as follows:
Discount = 0.001 x $100 = $0.10
The discount is $0.10.
Example 2: Calculating Interest
An investment account earns 0.1% interest per month. If the initial investment is $1,000, the interest earned in one month is:
Interest = 0.001 x $1,000 = $1.00
The interest earned is $1.00.
Example 3: Analyzing Survey Data
In a survey of 10,000 people, 0.1% responded with a particular answer. The number of people who gave that response is:
Number of Respondents = 0.001 x 10,000 = 10
Only 10 people gave that specific answer.
Working with Larger Percentages and Decimals: Extension of the Concept
The principles discussed above apply equally well to larger percentages. For example:
- 10% = 0.10
- 100% = 1.00
- 150% = 1.50
Notice that percentages greater than 100% result in decimal values greater than 1.
Converting Decimals Back to Percentages: The Reverse Process
Just as we can convert percentages to decimals, we can also reverse the process. To convert a decimal back to a percentage, simply multiply the decimal by 100 and add the percentage sign (%). Alternatively, move the decimal point two places to the right.
For example:
- 0.25 x 100 = 25%
- 0.001 x 100 = 0.1%
- 1.50 x 100 = 150%
This demonstrates the reciprocal relationship between decimals and percentages.
Frequently Asked Questions (FAQ)
Q1: What if I have a percentage with a fraction, like 0.5%?
A: Follow the same procedure. 0.5% = 0.5 ÷ 100 = 0.005. Simply divide the percentage value by 100.
Q2: Can I use a calculator to perform these conversions?
A: Yes, a calculator is a helpful tool for these conversions, particularly when dealing with more complex percentages.
Q3: Are there any shortcuts for converting percentages to decimals in my head?
A: The most common mental shortcut involves moving the decimal point two places to the left. This is often quicker than performing the division mentally.
Conclusion: Mastering Percentage to Decimal Conversion
Mastering the conversion between percentages and decimals is a crucial skill with widespread applications in various aspects of life. By understanding the fundamental principles of division by 100 or shifting the decimal point, you can confidently perform these conversions. This article has explored the process in detail, using clear examples and addressing common questions to solidify your understanding. Remember, consistent practice is key to mastering any mathematical concept, so continue practicing conversions to enhance your proficiency. With practice, these conversions will become second nature, enabling you to handle percentage-related calculations with ease and accuracy. This skill will undoubtedly prove invaluable as you progress in your mathematical and professional endeavors.
Latest Posts
Latest Posts
-
10000 Equals How Many Miles
Sep 18, 2025
-
1300 Dollars In Pakistani Rupees
Sep 18, 2025
-
Electric Field From Charge Density
Sep 18, 2025
-
32 Euros In Pounds Sterling
Sep 18, 2025
-
122cm Is How Many Inches
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 0.1 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.